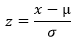Distribusi Normal

Distribusi normal, disebut pula distribusi Gauss, adalah distribusi probabilitas yang paling banyak digunakan dalam berbagai analisis statistika. Distribusi normal baku adalah distribusi normal yang memiliki rata-rata nol dan simpangan baku satu. Distribusi ini juga dijuluki kurva lonceng (bell curve) karena grafik fungsi kepekatan probabilitasnya mirip dengan bentuk lonceng.

Fungsi Pembangkit Momen ( FPM )

  misalkan

sehingga didapatkan 

dan

d 

sehingga

Mean / Ekspektasi (X)

Nilai mean ini merupakan turunan pertama dari fungsi pembangkit moment

  

Nilai Ekspektasi  X²

 Nilai Ekspektasi  X² ini merupakan turunan kedua dari fungsi pembangkit moment

 

Varians  (X) = Nilai harapan (X – E(X))²

^{Pustaka :}

^{https://id.wikipedia.org/wiki/Distribusi_normal}

^{http://www.rumusstatistik.com/2016/04/mgf-distribusi-normal.html} 

Distribusi Poisson

Dalam teori probabilitas dan statistika, distribusi Poisson (dilafalkan [pwasɔ̃]) adalah distribusi probabilitas diskret yang menyatakan peluang jumlah peristiwa yang terjadi pada periode waktu tertentu apabila rata-rata kejadian tersebut diketahui dan dalam waktu yang saling bebas sejak kejadian terakhir. (distribusi Poisson juga dapat digunakan untuk jumlah kejadian pada interval tertentu seperti jarak, luas, atau volume).

 

Fungsi Pembangkit Momen ( FPM ) Distribusi Poisson

 

Mean / Ekspektasi (X)

Nilai mean ini merupakan turunan pertama dari fungsi pembangkit moment

 

Nilai Ekspektasi  X²

 Nilai Ekspektasi  X² ini merupakan turunan kedua dari fungsi pembangkit moment

 

 

Varians  (X) = Nilai harapan (X – E(X))²

Pustaka :

https://id.wikipedia.org/wiki/Distribusi_Poisson

http://www.rumusstatistik.com/2016/04/mgf-distribusi-poisson.html

Distribusi Bernoulli

Dalam teori probabilitas dan statistika, distribusi binomial adalah distribusi probabilitas diskret jumlah keberhasilan dalam n percobaan ya/tidak (berhasil/gagal) yang saling bebas, dimana setiap hasil percobaan memiliki probabilitas p. Eksperimen berhasil/gagal juga disebut percobaan bernoulli. Ketika n = 1, distribusi binomial adalah distribusi bernoulli. Distribusi binomial merupakan dasar dari uji binomial dalam uji signifikansi statistik.

Fungsi Kepadatan Peluang

 


 

Fungsi Pembangkit Momen (MGF)
Mx(t) = 1 – p + pe^t

Rata-rata E(X) = p 
Rata-rata dari fungsi distribusi bernoulli merupakan turunan pertama dari FPM nya

E (X²) =  Nilai harapan X²  

Ekspektasi X²   dari fungsi distribusi bernoulli merupakan turunan kedua dari FPM nya

Varians  (X) = Nilai harapan (X – E(X))²

 

Pustaka :
https://id.wikipedia.org/wiki/Distribusi_binomial

http://www.rumusstatistik.com/2015/08/nilai-harapan-distribusi-bernoulli.html